- Tardigrade
- Question
- Physics
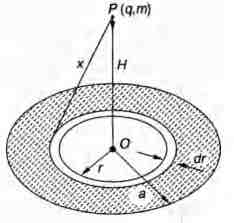
- A non-conducting disc of radius a and uniform positive surface charge density σ is placed on the ground with its axis vertical. A particle of mass m and positive charge q is dropped, along the axis of the disc from a height H with zero initial velocity. The particle has q/m = 4 ε0g/ σ. (a) Find the value of H if the particle just reaches the disc. (b) Sketch the potential energy of the particle as a function of its height and find its equilibrium position.
Q.
A non-conducting disc of radius a and uniform positive
surface charge density is placed on the ground with its axis
vertical. A particle of mass m and positive charge q is
dropped, along the axis of the disc from a height H with zero
initial velocity. The particle has q/m
(a) Find the value of H if the particle just reaches the disc.
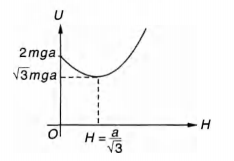
(b) Sketch the potential energy of the particle as a function
of its height and find its equilibrium position.
Solution:
Potential at a height H on the axis of the disc V (P )
The charge dq contained in the ring shown in figure
Potential at P due to this ring
Potential due to the complete disc
Potential at centre, (O) will be
(a) Particle is released from P and it just reaches point O.
Therefore, from conservation of mechanical energy
Decrease in gravitational potential energy = Increase in
electr ostatic potential energy
or
Substituting in Eq. (i), we get
or
or
or
or
or
(b) Potential energy of the particle at height
// = Electrostatic potential energy + gravitational
potential energy
Here V = Potential at height H
At equilibrium position
Differentiating Eq. (ii) w.r.t. H
or
or
or
or
or
From Eq. (ii), we can write
U - H equation as
(Parabolic variation)
U = 2 mga at H = 0
and
Therefore, U - H graph will be as shown
Note that at
Therefore, is stable equilibrium position.