Question

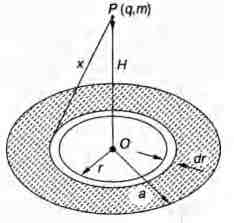
A non-conducting disc of radius a and uniform positive
surface charge density $\sigma $ is placed on the ground with its axis
vertical. A particle of mass m and positive charge q is
dropped, along the axis of the disc from a height H with zero
initial velocity. The particle has q/m $= 4 \varepsilon_0g/ \sigma. $
(a) Find the value of H if the particle just reaches the disc.
(b) Sketch the potential energy of the particle as a function
of its height and find its equilibrium position.

Answer 1

Potential at a height H on the axis of the disc V (P )
The charge dq contained in the ring shown in figure
$dq=(2 \pi r dr) \sigma $
Potential at P due to this ring
$dV= \frac {1}{4 \pi \varepsilon_0}. \frac {dq}{x} \, where \, x=\sqrt {H^2+r^2} $
$dV= \frac {1}{4 \pi \varepsilon_0}. \frac {(2 \pi rdr)\sigma}{\sqrt {H^2+r^2}}= \frac {\sigma}{2 \varepsilon_0}\frac {rdr}{\sqrt {H^2+r^2}} $
$\therefore $ Potential due to the complete disc
$V_p= \int _{r=0}^{r=a}dV $
$\, \, \, \, \, = \frac {\sigma}{2 \varepsilon_0}\int _{r=0}^{r=a} \frac {rdr}{\sqrt {H^2+r^2}} $
$V_p= \frac {\sigma}{2 \varepsilon_0}[\sqrt {a^2+H^2}-H] $
Potential at centre, (O) will be
$ V_0= \frac {\sigma a}{2 \varepsilon_0} H=0 $
(a) Particle is released from P and it just reaches point O.
Therefore, from conservation of mechanical energy
Decrease in gravitational potential energy = Increase in
electr ostatic potential energy
$(\Delta KE=0 \, because \, K_i=K_f=0) $
$\therefore \, \, \, \, \, \, \, mgH=q[V_0-V_p] $
or $gH= \bigg (\frac {q}{m}\bigg )\bigg (\frac {\sigma}{2 \varepsilon_0}\bigg )[a- \sqrt {a^2+H^2}+H] \, \, \, \, \, \, ...(i) $
$ \frac {q}{m}=\frac {4 \varepsilon_0g}{\sigma} $
$\therefore \frac {q \sigma}{2 \varepsilon_0m}=2g $
Substituting in Eq. (i), we get
$gH=2g[a+H- \sqrt {a^2+H^2}] $
or $ \frac {H}{2}=(a+H)- \sqrt {a^2+H^2} $
or $ \sqrt {a^2+H^2}=a+ \frac {H}{2} $
or $\, \, \, \, \, a^2+H^2=a^2+ \frac {H^2}{4}+aH $
or $\, \, \, \, \, \frac {3}{4}H^2=aH $
or $\, \, \, \, \, H= \frac {4}{3}a \, and \, H=0 $
$\therefore \, \, \, \, \, \, \, \, H=(4/3)a $
(b) Potential energy of the particle at height
// = Electrostatic potential energy + gravitational
potential energy
$\therefore U=qV+mgH $
Here V = Potential at height H
$U= \frac {\sigma q}{2 \varepsilon_0}[\sqrt {a^2+H^2}-H]+mgH \, \, \, \, \, \, \, \, \, \, ...(ii) $
At equilibrium position
$\, \, \, \, \, \, \, \, \, \, F= \frac {-dU}{dH}=0 $
Differentiating Eq. (ii) w.r.t. H
or $mg+ \sigma \frac {q}{2 \varepsilon_0}\bigg [\bigg (\frac {1}{2}\bigg )(2H) \frac {1}{\sqrt {a^2+H^2}}-1\bigg ]=0 $
$ \bigg (\because \frac {\sigma q}{2 \varepsilon_0}=2mg \bigg ) $
$\therefore \, \, \, mg+2mg \bigg [\frac {H}{\sqrt {a^2+H^2}}-1\bigg ]=0 $
or $\, \, \, \, \, \, \, 1+ \frac {2H}{\sqrt {a^2+H^2}}-2=0 $
or $\, \, \, \, \, \, \, \frac {2H}{\sqrt {a^2+H^2}}=1 $
or $\, \, \, \, \, \, \, \frac {H^2}{a^2+H^2}= \frac {1}{4} $
or $\, \, \, \, \, \, \, 3H^2=a^2 \, or \, H= \frac {a}{\sqrt 3} $
From Eq. (ii), we can write
U - H equation as
$\, \, \, \, \, \, \, \, U=mg(2 \sqrt {a^2+H^2}-H) $
(Parabolic variation)
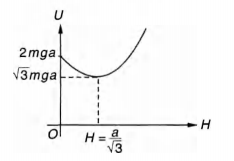
U = 2 mga at H = 0
and $U=U_{min}= \sqrt 3mga \, at \, H= \frac {a}{\sqrt 3} $
Therefore, U - H graph will be as shown
Note that at $H= \frac {a}{\sqrt 3}, U \, is \, minimum. $
Therefore, $H= \frac {a}{\sqrt 3} $ is stable equilibrium position.