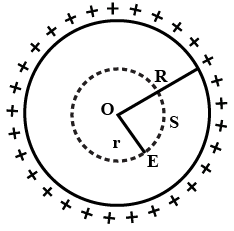
Question

A hollow insulated conduction sphere is given a positive charge of $10\mu C$. What will be the electric field at the center of the sphere if its radius is $2$ metres?

• A. Zero
• B. $5\mu C{m}^{-2}$
• C. $20\mu C{m}^{-2}$
• D. $8\mu C{m}^{-2}$

Answer 1

Answer: (A)

Step 1: Uniform Charge distribution on outer surface [Refer Figure]
As a property of conductor, Charge will resides on the outer surface of the hollow sphere. Since the shape of sphere is symmetric, hence charge distribution will be uniform, As shown in the figure.
Step 2: Finding Electric field inside
The given situation is now a uniformly charged hollow conducting shell.
Inside which the Electric field is zero at all points.
Alternate Solution using Gauss Law:
We can find the electric field inside using Gauss Law as follows:
Consider a gaussian spherical surface of radius $r<R$
Charge inside gaussian surface $q_{\text{in }}=0$
From gauss theorem:
$\oint \vec{E}\cdot \overrightarrow{ds}=\frac{q_{in}}{{\epsilon }_0}$
At all points of gaussian surface, $\vec{E}$ is constant radially outwards due to symmetry and $\overrightarrow{ds}$ is perpendicular to the gaussian surface, hence both are parallel and angle between them is zero.
$\therefore \vec{E}\oint \overrightarrow{ds}\cos 0^{\circ }=\vec{E}\oint \overrightarrow{ds}=\frac{q_{\text{in }}}{{\epsilon }_0}$
Full area of gaussian surface is $4\pi r^2$
$\Rightarrow E\times 4\pi r^2=\frac{1}{{\epsilon }_0}\times 0$
$\Rightarrow E=0$