- Tardigrade
- Question
- Physics
- A frame of reference that is accelerated with respect to an internal frame of reference is called a non-inertial frame of reference. A coordinate system fixed on a circular disc rotating about a fixed axis with a constant angular velocity ω is an example of a non-inertial frame of reference. The relationship between the force vecF text rot experienced by a particle of mass m moving on the rotating disc and the force vecF text in experienced by the particle in an internal frame of reference is vec F rot = vec F in +2 m ( vec v rot × vecω)+ m ( vecω × vec r ) × vecω where vec v rot is the velocity of the particle in the rotating frame of reference and vec r is the position vector of the particle with respect to the centre of the disc. Now consider a smooth slot along a diameter of a disc of radius R rotating counter-clockwise with a constant angular speed ω about its vertical axis through its center. We assign a coordinate system with the origin at the centre of the disc, the x-axis along the slot, the y-axis perpendicular to the slot and the z-axis along the rotation axis ( vecω=ω hatk). A small block of mass m is gently placed in the slot at vecr=((R/2)) hati at t=0 and is constrained to move only along the slot. <img class=img-fluid question-image alt=image src=https://cdn.tardigrade.in/img/question/physics/4bde75a0d47619cefeb4e6abe0551716-.png /> The distance r of the block at time t is
Q.
A frame of reference that is accelerated with respect to an internal frame of reference is called a non-inertial frame of reference. A coordinate system fixed on a circular disc rotating about a fixed axis with a constant angular velocity is an example of a non-inertial frame of reference.
The relationship between the force experienced by a particle of mass moving on the rotating disc and the force experienced by the particle in an internal frame of reference is
where is the velocity of the particle in the rotating frame of reference and is the position vector of the particle with respect to the centre of the disc.
Now consider a smooth slot along a diameter of a disc of radius rotating counter-clockwise with a constant angular speed about its vertical axis through its center. We assign a coordinate system with the origin at the centre of the disc, the -axis along the slot, the -axis perpendicular to the slot and the z-axis along the rotation axis . A small block of mass is gently placed in the slot at at and is constrained to move only along the slot.
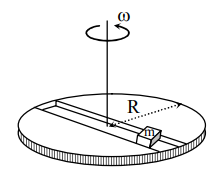
The distance of the block at time is
Solution: