Question

A frame of reference that is accelerated with respect to an internal frame of reference is called a non-inertial frame of reference. A coordinate system fixed on a circular disc rotating about a fixed axis with a constant angular velocity $\omega$ is an example of a non-inertial frame of reference.
The relationship between the force $\vec{F}_{\text {rot }}$ experienced by a particle of mass $m$ moving on the rotating disc and the force $\vec{F}_{\text {in }}$ experienced by the particle in an internal frame of reference is
$\vec{ F }_{ rot }=\vec{ F }_{ in }+2 m \left(\vec{ v }_{ rot } \times \vec{\omega}\right)+ m (\vec{\omega} \times \vec{ r }) \times \vec{\omega}$
where $\vec{ v }_{ rot }$ is the velocity of the particle in the rotating frame of reference and $\vec{ r }$ is the position vector of the particle with respect to the centre of the disc.
Now consider a smooth slot along a diameter of a disc of radius $R$ rotating counter-clockwise with a constant angular speed $\omega$ about its vertical axis through its center. We assign a coordinate system with the origin at the centre of the disc, the $x$-axis along the slot, the $y$-axis perpendicular to the slot and the z-axis along the rotation axis $(\vec{\omega}=\omega \hat{k})$. A small block of mass $m$ is gently placed in the slot at $\vec{r}=\left(\frac{R}{2}\right) \hat{i}$ at $t=0$ and is constrained to move only along the slot.

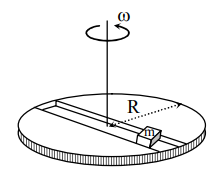
The distance $r$ of the block at time $t$ is

• A. $\frac{R}{2} \cos 2 \omega t$
• B. $\frac{ R }{2} \cos \omega t$
• C. $\frac{ R }{4}\left( e ^{ \omega t }+ e ^{-\omega t}\right)$
• D. $\frac{ R }{4}\left( e ^{2 \omega t }+ e ^{-2 \omega t}\right)$

Answer 1

Answer: (C)

Force on block along slot $=m \omega^{2} r$
$=m a=m\left(\frac{v d v}{d r}\right)$
$\int\limits_{0}^{V} v d v=\int\limits_{\frac{R}{2}}^{r} \omega^{2} r d r$
$\frac{v^{2}}{2}=\frac{\omega^{2}}{2}\left(r^{2}-\frac{R^{2}}{4}\right)$
$ \Rightarrow v=\omega \sqrt{r^{2}-\frac{R^{2}}{4}}=\frac{d r}{d t}$
$\Rightarrow \int\limits_{\frac{R}{4}}^{r} \frac{d r}{\sqrt{r^{2}-\frac{R^{2}}{4}}}=\int\limits_{0}^{t} \omega d t$
$\ln \left(\frac{\frac{r+\sqrt{r^{2}-\frac{R^{2}}{4}}}{R}}{2}\right) -\ln
\left(\frac{\frac{\frac{R}{2}+\sqrt{\frac{R^{2}}{4}-\frac{R^{2}}{4}}}{R}}{2}\right)=\omega t$
$\Rightarrow r+\sqrt{r^{2}-\frac{R^{2}}{4}}=\frac{R}{2} e^{\omega t}$
$\Rightarrow r^{2}-\frac{R^{2}}{4}=\frac{R^{2}}{4} e^{2 \omega t}+r^{2}-2 r \frac{R}{2} e^{\omega t}$
$\Rightarrow r=\frac{\frac{R^{2}}{4} e^{2 \omega t}+\frac{R^{2}}{4}}{R e^{\omega t}}=\frac{R}{4}\left(e^{\omega t}+e^{-\omega t}\right)$