Question

$Y \, (x,t)= \frac{0.8}{[(4x+5t)^2+5]} $ represents a moving pulse where $x$ and $y$ are in metre and $t$ is in second. Then

• A. pulse is moving in positive x-direction
• B. in 2 s it will travel a distance of 2.5 m
• C. its maximum displacement is 0.16 m
• D. it is a symmetric pulse

Answer 1

Answer: (B), (C), (D)

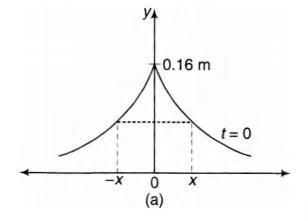
The shape of pulse at $x = 0$ and $t - 0$ would be as shown, in Fig. (a).
$y(0,0)= \frac {0.8}{5}=0.16\,m $
From the figure it is clear that $y_{max}=0.16\, m $
Pulse will be symmetric (Symmetry is checked about
$y_{max})$ if at $t=0 y(x) = y(-x) $
From the given equation,

Therefore, pulse is symmetric. Speed of pulse
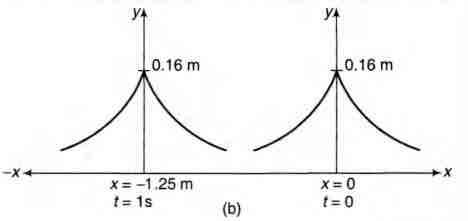
At $t = 1\, s$ and $x = - 1.25\, m$ value of $y$ is again $0.16\, m$,
i.e. pulse has travelled a distance of $1.25\, m$ in $1\, s$ in negative $x$-direction or we can say that the speed of pulse is $1.25\, m/s$ and it is travelling in negative $x$-direction.
Therefore, it will travel a distance of $2.5\, m$ in $2\, s$.
The above statement can be better understood from Fig. (b).