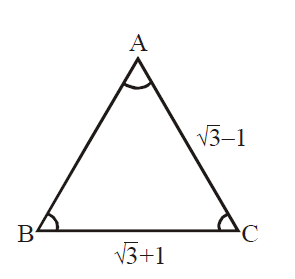
Q. With the usual notation, in $\Delta ABC$, if $\angle A + \angle B = 120^{\circ} , a = \sqrt{3} + 1$ and $b = \sqrt{3} - 1 $ , then the ratio $\angle A : \angle B$ , is :
Solution:
$A + B = 120^{\circ}$
$\tan \frac{A-B}{2} = \frac{a-b}{a+b} \cot\left(\frac{C}{2}\right) $
$= \frac{\sqrt{3}+1-\sqrt{3}+1}{2\left(\sqrt{3}\right)}\cot\left(30^{\circ}\right) = \frac{1}{\sqrt{3}}. \sqrt{3}=1$
$ \frac{A-B}{2} = 45^{\circ} \Rightarrow A-B =90^{\circ} $
$ A + B = 120^{\circ} $
$ ------$
$ 2A = 210^{\circ}$
$ A = 105^{\circ} $
$ B = 15^{\circ}$