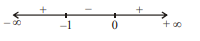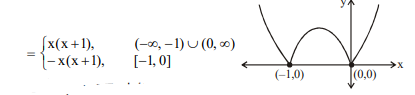Question

Which of the following statements is/are correct?
[Note: Q denotes the set of rational numbers.]

• A. If $f(x)=x^2+10 \sin x$, then there exist a real number $c$ such that $f(c)=1000$.
• B. $\frac{ d }{ dx }\left| x ^2+ x \right|=|2 x +1| \forall x \hat{\imath}$.
• C. If $y=f(x)$ and $x=g(y)$, where $g=f^{-1}$, then $\frac{d^2 x}{d y^2}=\frac{\left(\frac{d^2 y}{d x^2}\right)}{\left(\frac{d y}{d x}\right)^3}, \frac{d y}{d x} \neq 0$.
• D. Let $f:(0,5) \rightarrow R-Q$ be a continuous function such that $f(2)=\pi$, then $f(\pi)=\pi$.

Answer 1

Answer: (A), (D)

(A) Given $f ( x )= x ^2+10 \sin x \forall x \in R$
Also, $f(0)=0$ and $f(x)$ is continuous on $R$.
$\underset{x \rightarrow \pm \infty}{\text{Lim}} f ( x ) \rightarrow \infty \Rightarrow$ there exists some real number c such that $f ( x )=1000$
(Using intermediate value theorem).
(B) Let $f ( x )=\left| x ^2+ x \right|=| x ( x +1)| $


So, $f ( x )$ is non-derivable at two points viz $x =-1,0$.
(C) If $y=f(x)$ and $x=g(y)$ where $g=f^{-1}$, then
$\frac{d^2 x}{d y^2}=-\frac{\frac{d^2 y}{d x^2}}{\left(\frac{d y}{d x}\right)^3}, \frac{d y}{d x} \neq 0 .$
(D) As $f ( x )$ is continuous on $(0,5)$ and $f ( x )$ takes only irrational values such that $f (2)=\pi$, so $ f(\pi)=\pi($ As $f(x)$ must be only constant function).