Question

Which of the following are correct?
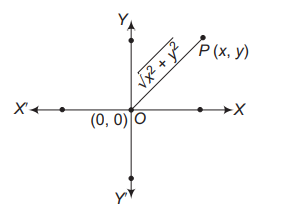
I. The modulus of complex number $x+i y=\sqrt{x^2+y^2}$
II. If $z=x+i y$, then modulus $Z$ is distance of the point from the origin.
III. Complex numbers which lie on $X$-axis are in the form of $a+i 0$.
IV. Complex numbers which lie on $Y$-axis are in the form of $0+b i$.

• A. I and II are correct
• B. II and III are correct
• C. I, II and III are correct
• D. All are correct

Answer 1

Answer: (D)

In the Argand plane, the modulus of the complex number $x+i y=\sqrt{x^2+y^2}$ is the distance between the point $P(x, y)$ and the origin $O(0,0)$. The points on the $X$-axis corresponds to the complex numbers of the form $a+i 0$ and the points on the $Y$-axis corresponds to the complex numbers of the form $0+i b$.

The $X$-axis and $Y$-axis in the Argand plane are called, respectively, the real axis and the imaginary axis.