Q.
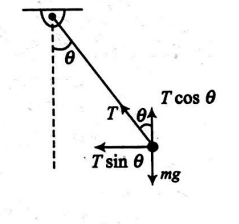
When the string of a conical pendulum makes an angle of $45^{\circ}$ with the vertical, its time period is $T_{1}$. When the string makes an angle of $60^{\circ}$ with the vertical, its time period is $T_{2}$. Then $T_{1}^{2} / T_{2}^{2}$ is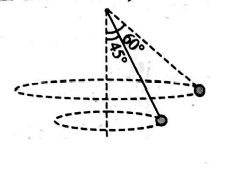
Laws of Motion
Solution:
$
\begin{array}{l}
T \cos \theta=m g=\text { constant } \\
\Rightarrow T_{1} \cos \theta_{1}=T_{2} \cos \theta_{2} \\
\frac{T_{1}}{T_{2}}=\frac{\cos \theta_{2}}{\cos \theta_{1}} \frac{\cos 60}{\cos 45} \\
=\frac{1 / 2}{1 / \sqrt{2}}=\frac{1}{\sqrt{2}} \\
\Rightarrow\left(\frac{T_{1}}{T_{2}}\right)^{2}=\frac{1}{2}
\end{array}
$
Along radial direction,
$
\begin{array}{l}
T_{1} \sin \theta_{1}=m \omega_{1}^{2} r_{1} \text { and } \\
T_{2} \sin \theta_{2}=m \omega_{2}^{2} r_{2} \\
\Rightarrow \frac{\omega_{1}^{2}}{\omega_{2}^{2}}=\frac{T_{1} \sin \theta_{1}}{T_{2} \sin \theta_{2}} \times \frac{r_{2}}{r_{1}}
\end{array}
$
Also from question diagram,
$r_{1}=\left|\sin \theta_{1} \& r_{2}=\right| \sin \theta_{2}$ where $\mid$ is the length of the string.
$
\Rightarrow \frac{r_{1}}{r_{2}}=\frac{\sin \theta_{1}}{\sin \theta_{2}}
$
$\therefore \frac{\omega_{1}^{2}}{\omega_{2}^{2}}=\frac{T_{1}}{T_{2}}$ and since time period $t=\frac{2 \pi}{\omega}$,
$
\frac{t_{1}}{t_{2}}=\frac{\omega_{2}}{\omega_{1}}=\sqrt{\frac{T_{2}}{T_{1}}}=\sqrt{2}
$