Q.
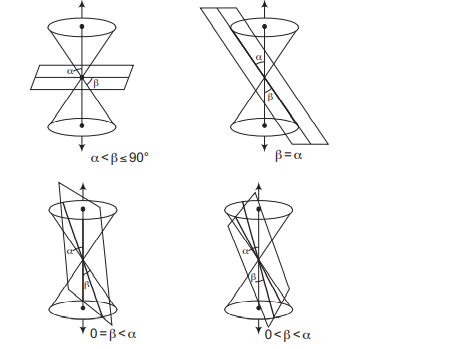
When the plane cuts at the vertex of the cone, then we have the following situations.
Column I
Column II
A
When $\alpha<\beta \leq 90^{\circ}$
1
Section is a pair of intersecting straight lines. (degenerate case of hyperbola)
B
When $\beta=\alpha$
2
Section is a point.
C
When $0 \leq \beta<\alpha$
3
Plane contains a generator of the cone and the section is a straight line. (degenerate case of parabola)
Here, $\beta$ is the angle made by the intersecting plane with the vertical axis of cone and $\alpha$ is the angle between the generator and vertical axis of cone.
Then, match the terms of Column I with terms of Column II and choose the correct option from the codes given below.
| Column I | Column II | ||
|---|---|---|---|
| A | When $\alpha<\beta \leq 90^{\circ}$ | 1 | Section is a pair of intersecting straight lines. (degenerate case of hyperbola) |
| B | When $\beta=\alpha$ | 2 | Section is a point. |
| C | When $0 \leq \beta<\alpha$ | 3 | Plane contains a generator of the cone and the section is a straight line. (degenerate case of parabola) |
Conic Sections
Solution:
A. When $\alpha<\beta \leq 90^{\circ}$, then section is a point.
B. When $\beta=\alpha$, the plane contains a generator of the cone and the section is a straight line.
It is the degenerate case of parabola.
C. When $0 \leq \beta<\alpha$, the section is a pair of intersecting straight lines. It is the degenerate case of a hyperbola.