1. Tardigrade
  2. Question
  3. Physics
  4. When resonance is produced in a series LCR circuit, then which of the following is not correct?

Question Error Report

Thank you for reporting, we will resolve it shortly

Back to Question

Q. When resonance is produced in a series $LCR$ circuit, then which of the following is not correct?

JIPMERJIPMER 2016Alternating Current

Solution:

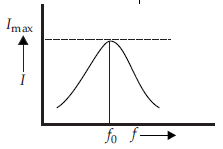
If $f_0$ is the resonance frequency corresponding to resonant angular frequency $\omega_0$, then $f_0 = \frac{\omega_0}{2 \pi} = \frac{1}{2 \pi \sqrt{LC}} \left( \because \, \omega_0 = \frac{1}{\sqrt{LC}} \right)$
The above eqn. is called the condition for resonance in the $LCR$ circuit. Figure shows the variation of current with frequency of the source. It follows that for $f = f_0$, the current in the circuit is maximum and hence, impedance of the circuit is minimum.

Solution Image