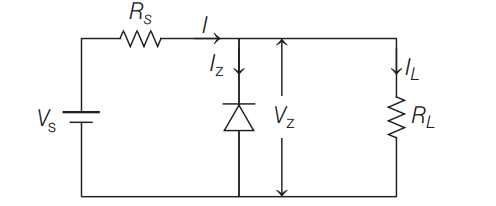
Question

When a zener diode is used as a regulator with zener voltage of $10 \,V$, nearly five times the load current passes through the zener diode. What should be the series resistance for the zener diode. If load resistance is $2\, k \,\Omega$ and the unregulated voltage supplied is $16\, V$.

• A. $500 \,\Omega$
• B. $100 \,\Omega$
• C. $200 \,\Omega$
• D. $800 \,\Omega$

Answer 1

Answer: (C)

According to the question, the circuit diagram of zener diode as a voltage regulator is shown below,

Given, voltage supply, $V_{s}=16 \,V$, voltage across
zener diode, $V_{Z}=10\, V$, current passes through the
zener diede, $I_{Z}=5 I_{L}$ and load resistance $R_{L}=2\, k\, \Omega$
The current through load resistance is
$I_{L} =\frac{\text { voltage }\left(V_{Z}\right)}{\text { resistance }\left(R_{L}\right)} $
$=\frac{10}{2 \times 10^{3}} $
$=5 \times 10^{-3} A\,\,\,...(i)$
The current through in the resistance in series
$I =I_{Z}+I_{L} $
$=5 I_{L}+I_{L}$
$=6 I_{L} $
$=6 \times 5 \times 10^{-3}$ [From Eq.(i)]
$=3 \times 10^{-2} A$
Also,$I=\frac{V_{S}-V_{Z}}{R_{S}} $
$\Rightarrow R_{S} =\frac{V_{S}-V_{Z}}{I} \,\,\,...(ii)$
substituting the values in Eqs. (ii), we get
$R_{S}=\frac{16-10}{3 \times 10^{-2}}=\frac{6}{3 \times 10^{-2}}=200\, \Omega$
Thus, the series resistance for zener diode is $200 \,\Omega$.