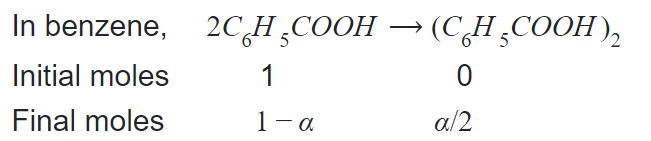Question

When $2.44$ grams of benzoic acid $\left( C _{6} H _{5} COOH \right)$ dissolved in $25$ grams of benzene, it shows depression of freezing point equal to $2.2\, K$. Molal depression constant of benzene is $5.0\, K\,kg \,mol ^{-1}$. What is the percentage association of acid, if it forms dimer in solution?

• A. $50 \%$
• B. $77 \%$
• C. $95 \%$
• D. $90 \%$

Answer 1

Answer: (D)

Given

Total number of moles of equilibrium $=1-\alpha+\alpha / 2$
$=1-\alpha / 2$
$\therefore i=\frac{\text { Total moles at equilibrium }}{\text { Initial moles }}=\frac{1-\alpha / 2}{1}$
We know that, $\Delta T_{f}=i K_{f} m$
$2 \cdot 2=\left(1-\frac{\alpha}{2}\right) \times 5.0\, k\, kg\,mol ^{-1} \times \frac{2.44}{122} \times \frac{1000}{25}$
$1-\frac{\alpha}{2}=\frac{2.2 \times 122 \times 25}{244 \times 1000 \times 5}$
$\Rightarrow 1-\frac{\alpha}{2}=0.55$
$\alpha=0.90$
Percentage degree of association $=90 \%$