Question

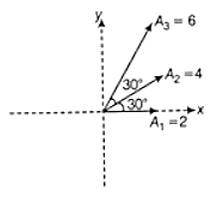
What will be the displacement equation of the simple harmonic motion obtained by combining the motions?

$x_{1}=2sin \omega t, \, \, x_{2}=4sin ⁡ \left(\omega t + \frac{\pi }{6}\right) \, and \, x_{3}=6sin ⁡ \left(\omega t + \frac{\pi }{3}\right)$

• A. $x=10.25sin \left(\omega t + \phi\right)$
• B. $x=10.25sin \left(\omega t - \phi\right)$
• C. $x=11.25sin \left(\omega t + \phi\right)$
• D. $x=11.25sin \left(\omega t - \phi\right)$

Answer 1

Answer: (C)

The resultant equation is
$x=Asin \left(\omega t + \phi\right)$
$\displaystyle \sum A_{x}=2+4cos 30^\circ +6cos⁡60^\circ =8.46$

And $\displaystyle \sum A_{y}=4sin 30^\circ +6cos⁡30^\circ =7.2$
$\therefore \, \, \, A=\sqrt{\left(\displaystyle \sum A_{x}\right)^{2} + \left(\displaystyle \sum A_{y}\right)^{2}}$
$= \, \, \sqrt{\left(8.46\right)^{2} + \left(7.2\right)^{2}}=11.25$
And $tan \phi=\frac{\displaystyle \sum A_{y}}{\displaystyle \sum A_{x}}=\frac{7.2}{8.46}=0.85$
$\Rightarrow \quad \phi=\tan ^{-1}(0.85)=40.4^{\circ}$
Thus, the displacement equation of combined motion is
$x=11.25sin \left(\omega t + \phi\right)$
Where, $\phi=40.4^\circ $