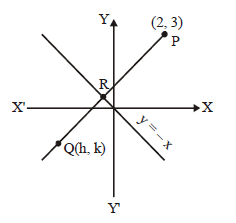
Q. What is the image of the point (2, 3) in the line y = - x ?
Straight Lines
Solution:
Let there be a point P(2,3) on cartesian plane.
Image of this point in the line y = -x will lie on a line which is perpendicular to this line and distance of this point from y = -x will be equal to distance of the image from this line.
Let Q be the image of p and let the co-ordinate of Q be (b, k)
Slope of line y = -x is -1
Line joining P, Q will be perpendicular to y = -x so, its slope = 1.
Let the equation of the line be y = x + c since this passes through point (2, 3)
3 = 2 + c $\rightarrow$ c = 1 and the equation y = x + 1
The point of intersection R lies in the middle of P & Q. Point of intersection of line y = - x and y = x + 1 is
$2 y = 1 , \Rightarrow \, y = \frac{1}{2}$ and $x = - \frac{1}{2}$
Hence, $\frac{h +2}{2} = - \frac{1}{2}$ and $\frac{k + 3}{2} = \frac{1}{2}$
$\Rightarrow \, h = -3$ and $k = - 2$
So, the image of the point (2, 3) in the y = - x is ( -3, -2).