Q.
What is the direction of the electric field at the centre $O$ of the square in the figure shown below? Given that, $q=10\, n C$ and the side of the square is $5\, cm$.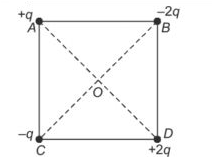
ManipalManipal 2020
Solution:
