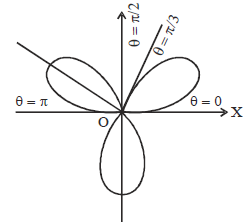
Q. What is the area of a loop of the curve $r=a \sin 3 \theta$ ?
VITEEEVITEEE 2016
Solution:
If curve $r = a \sin \, 3\theta$
To trace the curve, we consider the following table :
$3\theta = $
$ 0$
$ \frac{\pi}{2} $
$\pi $
$ \frac{ 3 \pi}{2} $
$2 \pi $
$ \frac{5 \pi}{2} $
$3 \pi $
$\theta = $
$0$
$ \frac{\pi}{6} $
$ \frac{\pi}{3} $
$ \frac{ \pi}{2} $
$ \frac{2\pi}{3} $
$ \frac{5 \pi}{6} $
$\pi $
$r =$
$0$
$a$
$0$
$-a$
$0$
$a$
$ 0$
Thus there is a loop between $\theta=0$ and $\theta=\frac{\pi}{3}$ as $r$ varies from $r=0$ to $r=0$.
Hence, the area of the loop lying in the positive quadrant $=\frac{1}{2} \int\limits_{0}^{\frac{\pi}{3}} r ^{2} d \theta$
$=\frac{ a ^{2}}{2} \int\limits_{0}^{\frac{\pi}{2}} \sin ^{2} \phi \cdot \frac{1}{3} d \phi$
[On putting, $3 \theta=\phi \Rightarrow d \theta=\frac{1}{3} d \phi$ ]
$=\frac{ a ^{2}}{6} \int\limits_{0}^{\frac{\pi}{2}} \sin ^{2} \phi \,d \,\phi$
$=\frac{ a ^{2}}{6} \cdot \int\limits_{0}^{\frac{\pi}{2}} \frac{1-\cos 2 \phi}{2} d \phi$
$\left[\because \cos 2 \theta=1-2 \sin ^{2} \theta\right]$
$=\frac{ a ^{2}}{12} \cdot\left[\phi+\frac{\sin 2 \phi}{2}\right]_{0}^{\frac{\pi}{2}}$
$=\frac{ a ^{2}}{12} \cdot\left[\frac{\pi}{2}+\frac{\sin \pi}{2}\right]=\frac{ a ^{2} \pi}{24} .$
| $3\theta = $ | $ 0$ | $ \frac{\pi}{2} $ | $\pi $ | $ \frac{ 3 \pi}{2} $ | $2 \pi $ | $ \frac{5 \pi}{2} $ | $3 \pi $ |
| $\theta = $ | $0$ | $ \frac{\pi}{6} $ | $ \frac{\pi}{3} $ | $ \frac{ \pi}{2} $ | $ \frac{2\pi}{3} $ | $ \frac{5 \pi}{6} $ | $\pi $ |
| $r =$ | $0$ | $a$ | $0$ | $-a$ | $0$ | $a$ | $ 0$ |