Question

We define average current as $I_{ av }=\frac{\Delta Q }{\Delta t}$ and instantaneous current as $I=\frac{d Q}{d t}$. Obviously, $Q=\int I d t$. Further, electric energy delivered per unit time by a source, i.e., power, $P=\frac{\Delta E}{\Delta t}$, where $\Delta E$ is the energy delivered by the source in time $\Delta t$.
In a certain accelerator, electrons emerge with energies of $40.0 MeV \left(1 MeV =1.60 \times 10^{-13} J \right)$. The electrons do not emerge in steady stream, but in pulses that repeat 250 times per second.

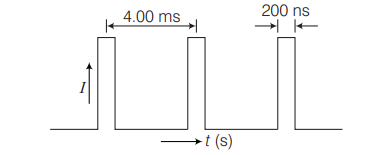
This corresponds to a time between each pulse of $4.00 ms$ in figure. Each pulse lasts for $200 ms$ and the electrons in the pulse constitute a current of $250 mA$. The current is zero between the pulses. While the pulse is on, the current is constant.
The maximum power delivered by the electron beam is

• A. $100 W$
• B. $10 kW$
• C. $1 MW$
• D. $10 MW$

Answer 1

Answer: (D)

Maximum power delivered by the electron beam
$P =\frac{\Delta E}{\Delta t}$
$=\frac{\left(3.13 \times 10^{11} { electrons } / \text { pulse }\right)(40.0 MeV / { electron })}{2.00 \times 10^{-7} s / { pulse }}$
$=\left(6.26 \times 10^{19} MeV / s \right)\left(1.6 \times 10^{-13} J / MeV \right) $
$=1.00 \times 10^{7} W =10.0 MW$