Q.
Water is flowing through a channel (lying in a vertical plane) as shown in the figure. Three sections $A, B$ and $C$ are shown. Sections $B$ and $C$ have equal area of cross section. If $P_{A}, P_{B}$ and $P_{C}$ are the pressures at $A, B$ and $C$. respectively then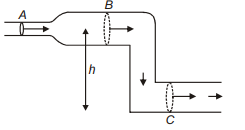
Mechanical Properties of Fluids
Solution: