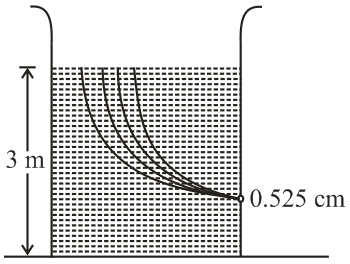
Question

Water is filled in a cylindrical container to a height of $3\,m.$ The ratio of the cross-sectional area of the orifice and the beaker is $0.1.$ The square of the speed of the liquid coming out from the orifice is $\left(g = 10 \,m / s^{2}\right)\ldots \ldots m^{2}/s^{2}.$

Answer 1

Let $v$ be velocity of efflux and $v'$ be the velocity of fall of liquid level in tank. Using equation of continuity for tube of flow formed between level of tank and orifice is
$Av'=av...\left(i\right)$

Applying Bernoulli's theorem, we have
$\frac{p}{\rho }+\frac{1}{2}\left(v^{'}\right)^{2}+gh=\frac{p}{\rho }+\frac{1}{2}v^{2}+0$
From equation $v^2=\frac{2 g h}{1-\frac{a^2}{A}}=\frac{2 \times 10 \times(3-0.525)}{1-(0.1)^2}$ $\Rightarrow v^2=50\, m ^2 s ^{-2}$