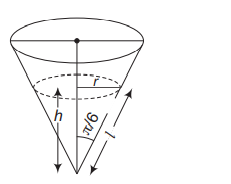
Question

Water is dripping out at a steady rate of $1\, cm ^3 / s$ through a tiny hole at the vertex of the conical vessel, whose axis is vertical. If the slant height of water in the vessel is $4\, cm$, then the rate of decrease of slant height, where the vertical angle of the conical vessel is $\frac{\pi}{3}$, is

• A. $\frac{1}{2 \sqrt{3} \pi} cm / s$
• B. $2 \sqrt{3} \pi cm / s$
• C. $\sqrt{3} \pi cm / s$
• D. None of these

Answer 1

Answer: (A)

Given that, $\frac{d V}{d t}=-1 \,cm ^3 / s$, where $V$ is the volume of water in the conical vessel.
From the figure, $ I=4\, cm , h=I \cos \frac{\pi}{6}=\frac{\sqrt{3}}{2} l $ and $r=I \sin \frac{\pi}{6}=\frac{1}{2}$
Therefore, $V=\frac{1}{3} \pi r^2 h=\frac{1 \cdot \pi}{3}\left(\frac{l}{2}\right)^2 \cdot\left(\frac{\sqrt{3}}{2} l\right)=\frac{\sqrt{3}}{24} /^3 \pi$
$\frac{d V}{d t}=\frac{\sqrt{3} \pi}{8} l^2 \frac{d l}{d t}$

Therefore, $ -1=\frac{\sqrt{3} \pi}{8} 16 \cdot \frac{d l}{d t} $
$\Rightarrow \frac{d l}{d t}=\frac{-1}{2 \sqrt{3} \pi} cm / s $
Therefore, the rate of decrease of slant height $=\frac{1}{2 \sqrt{3} \pi} cm / s$.