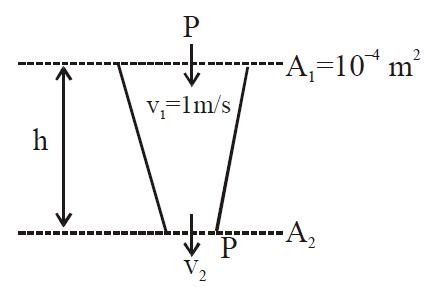Question

Water from a tap emerges vertically downwards with an initial speed of $1.0\, ms^{-1}$. The crosssectional area of the tap is $10^{-4} \; m^2$. Assume that the pressure is constant throughout the stream of water and that the flow is streamlined. The cross-sectional area of the stream, $0.15\, m$ below the tap would be :
(Take $g \,= \,10\, ms^{-2}$)

• A. $ 1 \times 10^{-5} \; m^2$
• B. $ 5 \times 10^{-5} \; m^2$
• C. $ 2 \times 10^{-5} \; m^2$
• D. $5 \times 10^{-4} \; m^2$

Answer 1

Answer: (B)

$A_{1}v_{1} =A_{2}v_{2}$
$ 10^{-4} \times1 = A_{2}v_{2} $
$A_{2}v_{2} =10^{-4} $ .......(1)
$P + \frac{1}{2} \rho\left(v_{1}^{2} -v_{2}^{2}\right) +\rho gh =P $
$ v_{2}^{2} =v_{1}^{2} +2gh $
$ v_{2} = \sqrt{v_{1}^{2} +2gh} $
$= \sqrt{1+2\times10 \times0.15} $
$ \frac{10^{-4}}{A_{2}} = 2 $
$A_{2} = 5 \times10^{-5} m^{2} $