Q.
Water flows in a horizontal tube (see figure). The pressure of water changes by $700\, Nm^{-2}$ between $A$ and $B$ where the area of cross section are $40\, cm^2$ and $20\, cm^2$, respectively. Find the rate of flow of water through the tube.
(density of water = $1000\, kgm^{-3}$)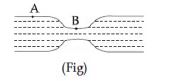
Solution: