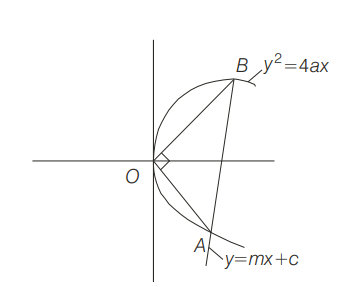Question

Variable straight lines $y = mx + c$ make intercepts on the curve $y^2 - 4ax = 0$ which subtend a right angle at the origin. Then the point of concurrence of these lines $y = mx + c$ is

• A. (4a, 0)
• B. (2a, 0)
• C. (- 4a, 0)
• D. ( - 2a, 0)

Answer 1

Answer: (A)

On homogenisation of the curve $y^{2}-4 a x=0$ by line $y=m x +c$, we are getting combined equation of straight lines which subtend a right angle at the origin, So

$y^{2}-4 a x\left(\frac{y-m x}{c}\right)=0$
$\Rightarrow c+4 a m=0$ ...(i)
On putting the value of $'c'$ in the line, we get $y=m(x-4 a)$, represent family of line passes through $(4 a, 0)$.