Question

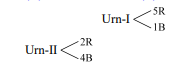
Urn-I contains 5 Red balls and 1 Blue ball,
Urn-II contains 2 Red balls and 4 Blue balls.
A fair die is tossed. If it results in an even number, balls are repeatedly withdrawn one at a time with replacement from urn-I. If it is an odd number, balls are repeatedly withdrawn one at a time with replacement from urn-II. Given that the first two draws both have resulted in a blue ball.
Conditional probability that the first two draws have resulted in blue balls given urn-II is used is

• A. $1 / 2$
• B. $4 / 9$
• C. $1 / 3$
• D. None

Answer 1

Answer: (B)

A: first two draws resulted in a blue ball.
$B _1 \text { : urn-I is used } \,\,\,\,\,\, P \left( B _1\right)=\frac{1}{2} $
$B _2 \text { : urn-II is used } \,\,\,\,\,\, P \left( B _2\right)=\frac{1}{2}$

$P \left( A / B _1\right)=\frac{1}{6} \cdot \frac{1}{6}=\frac{1}{36} $
$P \left( A / B _2\right)=\frac{4}{6} \cdot \frac{4}{6}=\frac{16}{36}=\frac{4}{9} $