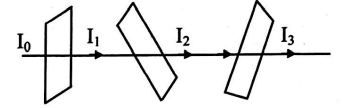
Question

Unpolarized light of intensity $32\, W / m ^{2}$ passes through three polarizers, such that the transmission axis of last polarizer is crossed with the first. If intensity of emerging light is $3\, W / m ^{2}$, what is the angle (in degree) between the transmission axis of the first two polarizers?

Answer 1

Let $\theta_{12}$ be the angle between the transmission axes of the first two polarizers $P_{1}$ and $P_{2}$ and $\theta_{23}$ be the angle between the transmission axes of polarizers $P_{2}$ and $P_{3}$.
Then $\theta_{12}+\theta_{23}=90^{\circ}$

$I _{0}=32\, W / m ^{2}$
Let $I_{1}, I_{2}$ and $I_{3}$ be the intensities of light on passing through the first, second and third polarizer, respectively.
Then, $I _{1}=\frac{1}{2} I _{0}$
$=\frac{1}{2} \times 32$
$=16\, W / m ^{2}$
From Malus law,
$I _{2}= I _{1} \cos ^{2} \theta_{12}$
$\Rightarrow I _{2} =16 \cos ^{2} \theta_{12}$
and $I _{3} = I _{2} \cos ^{2} \theta_{23}$
$=\left(16 \cos ^{2} \theta_{12}\right) \cos ^{2}\left(90^{\circ}-\theta_{12}\right)$ ...[From ()i]
$=16 \cos ^{2} \theta_{12} \sin ^{2} \theta_{12}$
$=4 \sin ^{2} 2 \theta_{12}$
But $I _{3} =3\, Wm ^{-2}$
$\Rightarrow 4 \sin ^{2} 2 \theta_{12}=3$
$\Rightarrow \sin 2 \theta_{12}=\frac{\sqrt{3}}{2}$
$\Rightarrow 2 \theta_{12}=60^{\circ}$
$\Rightarrow \theta_{12}=30^{\circ}$