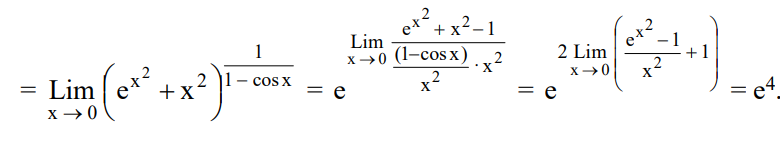Q. $\underset{x \rightarrow 0} {\text{Lim}} \frac{\int\limits_0^x\left(t^2+e^{t^2}\right)^{\frac{1}{1-\cos t}} d t}{\left(e^x-1\right)}$ is equal to
Integrals
Solution:
$L=\underset{x \rightarrow 0}{\text{Lim}} \frac{\int\limits_0^x\left(t^2+e^{t^2}\right)^{\frac{1}{1-\cos t}} d t}{x}\left(\frac{0}{0}\right)$