Question

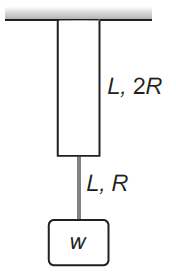
Two wires of the same material (Young's modulus $Y$ ) and same length $L$ but radii $R$ and $2 \,R$ respectively are joined end to end and a weight $w$ is suspended from the combination as shown in the figure. The elastic potential energy in the system is

• A. $\frac{3 w^{2} L}{4 \pi R^{2} Y}$
• B. $\frac{3 w^{2} L}{8 \pi R^{2} Y}$
• C. $\frac{5 w^{2} L}{8 \pi R^{2} Y}$
• D. $\frac{w^{2} L}{\pi R^{2} Y}$

Answer 1

Answer: (C)

$\text { As, } k_{1}=\frac{Y \pi(2 R)^{2}}{L} \text { and } k_{2}=\frac{Y \pi(R)^{2}}{L}$
Since, $k_{1} x_{1}=k_{2} x_{2}=w$
Elastic potential energy of the system
$U =\frac{1}{2} k_{1} x_{1}^{2}+\frac{1}{2} k_{2} x_{2}^{2}$
$=\frac{1}{2} k_{1}\left(\frac{w}{k_{1}}\right)^{2}+\frac{1}{2} k_{2}\left(\frac{w}{k_{2}}\right)^{2}$
$=\frac{1}{2} w^{2}\left\{\frac{1}{k_{1}}+\frac{1}{k_{2}}\right\}$
Now,$ \frac{1}{k_{1}}+\frac{1}{k_{2}}=\frac{L}{4 Y \pi R^{2}}+\frac{L}{Y \pi R^{2}} $
$\therefore U =\frac{1}{2} w^{2}\left(\frac{5 L}{4 Y \pi R^{2}}\right)=\frac{5 w^{2} L}{8 \pi Y R^{2}}$