Question

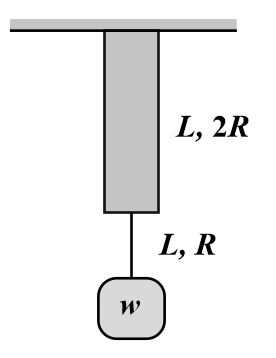
Two wires of the same material (Young's modulus $Y$ ) and same length $L$ but radii $R$ and $2R$ respectively are joined end to end and a weight $w$ is suspended from the combination as shown in the figure. The elastic potential energy in the system is

• A. $\frac{3 w^{2} L}{4 \pi R^{2} Y} \, $
• B. $\frac{3 w^{2} L}{8 \pi R^{2} Y}$
• C. $\frac{5 w^{2} L}{8 \pi R^{2} Y}$
• D. $\frac{w^{2} L}{\pi R^{2} Y} \, $

Answer 1

Answer: (C)

$k_{1}= \, \, \frac{Y\pi \left(2 R\right)^{2}}{L}$ , $k_{2}=\frac{Y\pi \left(R\right)^{2}}{L}$
Equivalent $\frac{1}{k_{1}}+\frac{1}{k_{2}}=\frac{L}{4 Y\pi R^{2}}+\frac{L}{Y\pi R^{2}}$
Since, $k_{1}x_{1}=k_{2}x_{2}=w$
Elastic potential energy of the system
$U =\frac{1}{2}k_{1}x_{1}^{2}+\frac{1}{2} \, k_{2}x_{2}^{2}$
$U=\frac{1}{2} \, k_{1}\left(\frac{w}{k_{1}}\right)^{2}+\frac{1}{2}k_{2}\left(\frac{w}{k_{2}}\right)^{2}$
$=\frac{1}{2}w^{2} \, \left\{\frac{1}{k_{1}} + \frac{1}{k_{2}}\right\}=\frac{1}{2}w^{2}\left(\frac{5 L}{4 \left(Y\pi R\right)^{2}}\right)$
$U =\frac{5 w^{2} L}{8 \pi YR^{2}}$