Q.
Two wires of equal length and equal cross sectional areas are suspended as shown in the figure. Their Young's modulii are $Y_{1}$ and $Y_{2}$, respectively. The equivalent Young's modulus is
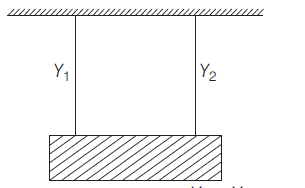
AP EAMCETAP EAMCET 2019
Solution:
