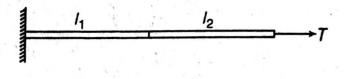
Question

Two wires of equal cross section, but one made up of steel and the other copper are joined end to end. When the combination is kept under tension, the elongations in the two wires are found to be equal. If ($Y$ for steel = $2.0\times 10^{11}\,Nm^{-2}$ and $Y$ for copper $= 1.1 \times 10^{11}\,Nm^{-2}$, the ratio of the lengths of the two wires is

• A. 20 : 11
• B. 11 : 20
• C. 5 : 4
• D. 4 : 5

Answer 1

Answer: (A)

Given, $ Y_{\text{steel}}= 2 \times 10^{11}\, N/m^2$
$Y_{\text{copper}} = 1. 1 \times 10^{11}\, N/m^2$
The wires are joined end to end.

$\Delta l_1 = \Delta l_2$
Also $T_1 = T_2$
The formula of Young’s modulus
$Y = \frac{Tl}{A\Delta l}$
$ \Rightarrow l = \frac{YA\Delta l}{T} $
$ \Rightarrow \frac{l_{1}}{l_{2}} = \frac{Y_{1}A_{1}\Delta l_{1}}{T_{1}} /\frac{Y_{2}A_{2}\Delta l_{2}}{T_{2}} $
$= \frac{Y_{1}A}{Y_{2}A} \left[\because A_{1} = A_{2}\right]$
$ \Rightarrow \frac{l_{1}}{l_{2}} = \frac{Y_{1}}{Y_{2}} $
$ =\frac{ 2 \times 10^{11}}{1.1\times 10^{11}} = \frac{20}{11} $