Question

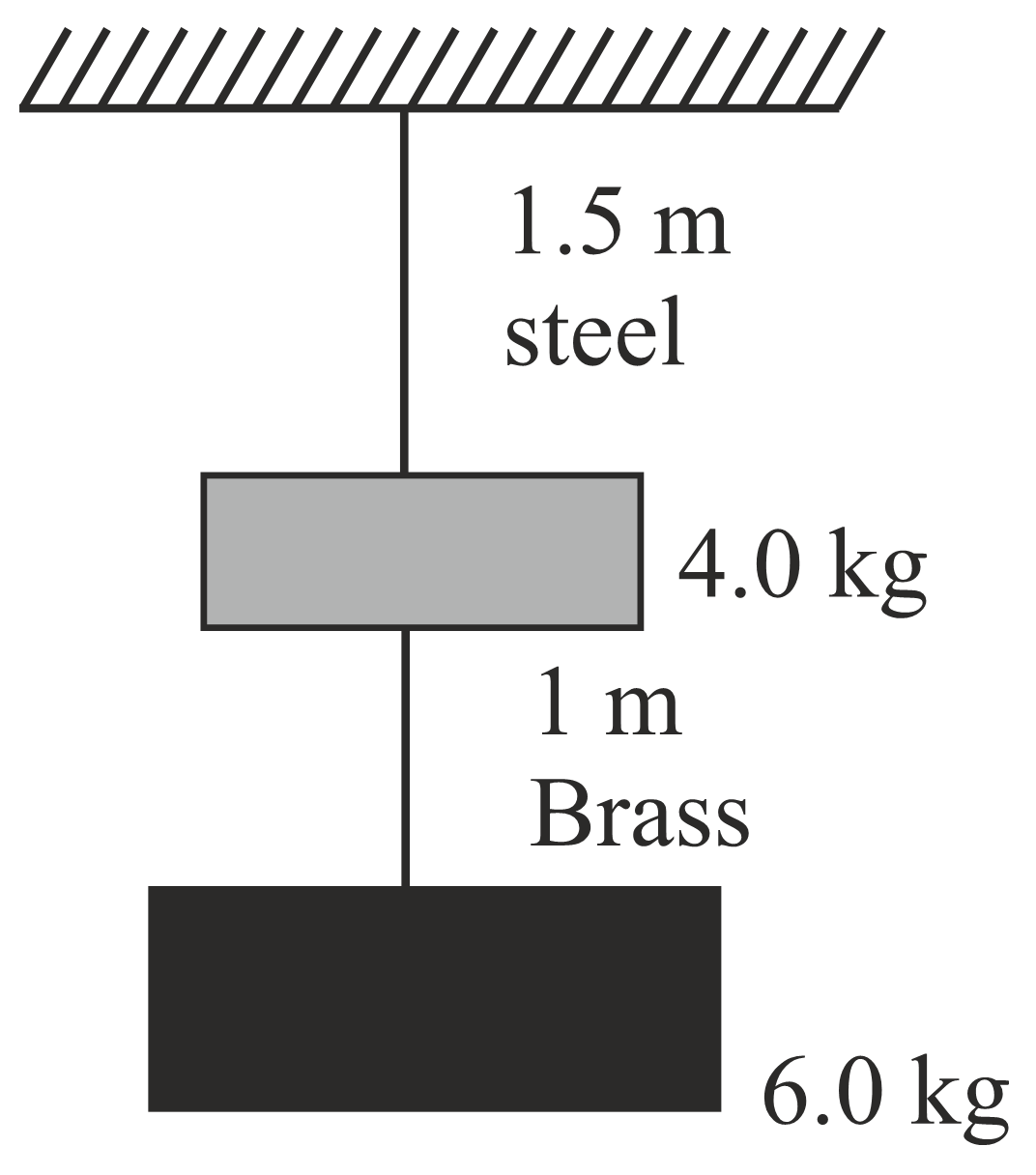
Two wires of diameter 0.25 cm, one made of steel and other made of brass are loaded as shown in figure. The unloaded length of steel wire is 1.5 m and that of brass wire is 1.0 m. Young's modulus of steel is 2.0 × 10¹¹ and Young's modulus of Brass 0.91 × 10¹¹ Pa. The elongations of steel and brass wires are respectively

• A. 1.3 × 10^-2 m;
  1.5 × 10^-4 m
• B. 1.5 × 10^-4 m;
  1.3 × 10^-4 m
• C. 2.0 × 10^-5 m;
  1.8 × 10^-3 m
• D. 1.8 × 10^-3 m;
  2.1 × 10^-3 m

Answer 1

Answer: (B)

Given, diameter of wires (2r) = 0.25 cm
r = 0.125 cm = 1.25 × 10^-3 m
For steel wire,
Load (F₁) = (4 + 6) kgf = 10 × 9.8 N = 98 N
Length of steel wire (l₁) = 1.5 m
Young's modulus $( Y )=\frac{ F _{1} \times l_{1}}{ A _{1} \times \Delta l_{1}}$ Change in length $\left(\Delta l_{1}\right)=\frac{ F _{1} \times l_{1}}{ A _{1} \times Y _{1}}$
$ \begin{array}{l} =\frac{ F _{1} \times l_{1}}{\pi r _{1}^{2} \times Y _{1}} \\ =\frac{98 \times 1.5}{3.14 \times\left(1.25 \times 10^{-3}\right)^{2} \times 2.0 \times 10^{11}} \\ =1.5 \times 10^{-4} m \end{array} $
For brass wire,
Load $\left(F_{2}\right)=6 kgf =6 \times 9.8 N =58.8 N$
Length of brass wire $\left(I_{2}\right)=1.0 m$
Young's modulus $\left(Y_{2}\right)=0.91 \times 10^{11} Pa$
Change in length $\left(l_{2}\right)=\frac{ F _{2} \times l_{2}}{\pi r _{2}^{2} \times Y _{2}}$
$ \begin{array}{l} =\frac{58.8 \times 1.0}{3.14 \times\left(1.25 \times 10^{-3}\right)^{2} \times 0.91 \times 10^{11}} \\ =1.3 \times 10^{-4} m \end{array} $