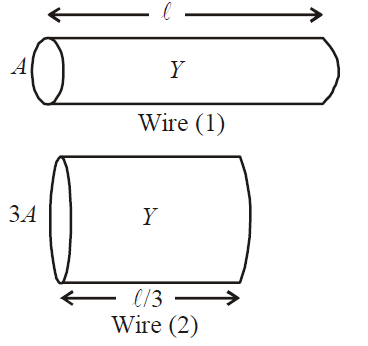
Q. Two wires are made of the same material and have the same volume. However wire $1$ has cross sectional area A and wire $2$ has cross-sectional area $3A$. If the length of wire $1$ increases by $\Delta x$ on applying force $F$, how much force is needed to stretch wire $2$ by the same amount?
BITSATBITSAT 2016
Solution:
As shown in the figure, the wires will have the same Young's modulus (same material) an the length of the wire of area of cross-section $3 A$ will be $1 / 3$ (same volume as wire 1 ).
For wire $1, Y=\frac{F / A}{\Delta x / 1} \ldots$ (i)
For wire $2, Y =\frac{ F ^{\prime} / 3 A }{\Delta x /(1 / 3)} \ldots$ (ii)
From (i) and (ii),
$\frac{F}{A} \times \frac{1}{\Delta x}=\frac{F^{\prime}}{3 A} \times \frac{1}{3 \Delta x} $
$\Rightarrow F^{\prime}=9 F$.