Question

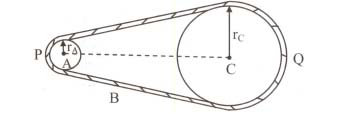
Two wheels $A$ and $C$ are connected by a belt $B$ . As denoted in the figure, the radius of $C$ is three times the radius of $A$ . If it is known that both the wheels have the same rotational kinetic energy, compute the ratio of their respective inertia $\left(\frac{I_{C}}{I_{A}}\right)$ .

Answer 1

As the belt does not slip, $v_p=v_Q$ i.e.,
$ r _{ A } \omega_{ A }= r _{ C } \omega_{ C } \ldots .(\because v = r \omega) \ldots \text { (i) } $
If $r_{ A }= r$, then $r_C=3 r$,
$ \therefore \omega_A=3 \omega_C \ldots[\operatorname{From}(i)] $
If both the wheels have the same rotational kinetic energy, then
$ \begin{array}{l} \frac{1}{2} I_A \omega_A^2=\frac{1}{2} I_C \omega_C^2 \\ \frac{ I _{ C }}{ I _{ A }}=\left[\frac{\omega_{ A }}{\omega_{ C }}\right]^2=\left[\frac{3}{1}\right]^2=\frac{9}{1} \end{array} $