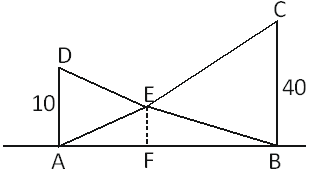
Question

Two vertical poles of height $10\,m$ and $40\,m$ stand apart on a horizontal plane. The height (in meters) of the point of intersection of the lines joining the top of each pole to the foot of the other, from this horizontal plane is

• A. $8$
• B. $10$
• C. $6$
• D. $4$

Answer 1

Answer: (A)

Let $A\left(0,0\right),D\left(0,10\right),$ $B\left(x_{1} , 0\right),C\left(x_{1} ,40\right)$

Equation of $AC\Rightarrow y=\frac{40}{x_{1}}x.... \left(1\right)$
Equation $BD\Rightarrow y-10=\frac{- 10}{x_{1}}x....\left(2\right)$
From $\left(1\right)$ and $\left(2\right)$ , we get,
$\frac{x_{1} \cdot y}{40}=\frac{- \left(y - 10\right) \cdot x_{1}}{10}$
$y=-4y+40\Rightarrow y=8$