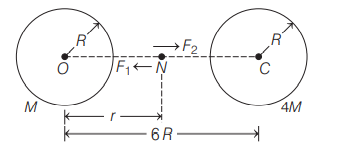
Question

Two uniform solid spheres of equal radii $R$ but mass $M$ and $4 M$ have a centre-to-centre separation $6 R$ as shown in figure. The two spheres are held fixed. A projectile of mass $m$ is projected from the surface of the sphere of mass $M$ directly towards the centre of the second sphere. $N$ is the point where net gravitational is zero.

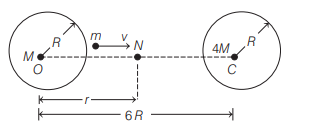
With reference to the above situation, match the Column I (quantities) with Column II (mathematical expressions) and select the correct answer from the codes given below.

Column I		Column II
A	Distance $r$ of neutral point $N$	1	$\sqrt{\frac{3 G M}{5 R}}$
B	Minimum speed of the projectile,$v_{\min }$, so that it reaches the surface of the second sphere.	2	$2 R$
C	The speed with which the projectile hits the seconds sphere, if projected with $v_{\min }$.	3	$\sqrt{\frac{27 G M}{5 R}}$

• A. $A -(1), B - (2), C -(3)$
• B. $A -(3), B - (2), C -(1)$
• C. $A -(2), B - (1), C -(3)$
• D. $A -(3), B - (1), C -(2)$

Answer 1

Answer: (C)

A. The projectile is acted upon by two mutually opposing gravitational forces of the two spheres. Hence, there must be a point on the line $O C$, where $F_{\text {ext }}=0$, i.e. net external force due to gravitational attraction force vanishes. The point is called neutral point $N$. Let it be at a distance $r$ from $O$.
$\Rightarrow O N=r$

At $N, F_{1}-F_{2}$
$\Rightarrow \frac{G m M}{r^{2}}=\frac{G m(4 M)}{(6 R-r)^{2}} $
$\Rightarrow r=2 R$ or $-6 R$
The neutral point $r=-6 R$ is not relevant.
Thus, $O N=r=2 R$.
B. To project the projectile with minimum speed from $M$. It is sufficient to project the particle with a speed which would enable it to reach $N$. After $N$,
projectile will be attracted by $4 \,M$.
At the neutral point, speed approaches zero,
i.e. $ v_{N}=0$
Total energy of the particle at $N=E_{N}$
$\Rightarrow E_{N} =\text { GPE due to } M+\text { GPE due to } 4 M $
$E_{N} =\frac{G m M}{2 R}-\frac{4 G M m}{4 R}$ ....(i)
$\left[\because\right.$ GPE due to $M=-\frac{GmM}{2 R} ; r=2 R$
GPE due to $4 M=-\frac{4 G M m}{4 R} ; r=4 R$ ]
From the principle of conservation of mechanical energy,
$\frac{1}{2} m v^{2}-\frac{G m M}{R}-\frac{4 G M m}{5 R}=-\frac{G M m}{2 R}-\frac{4 G M m}{4 R}$
$\Rightarrow v=\sqrt{\frac{3 G M}{5 R}}$
$\Rightarrow v_{\min }=\sqrt{\frac{3 G M}{5 R}}$
Therefore, minimum speed of the projectile with which it reaches the surface of second sphere is $\sqrt{\frac{3 G M}{5 R}}$.
C. Let $v_{f}$ be the speed with which projectile hits the second sphere. Applying principle of conservation of energy, we get
$\Rightarrow v_{f}=\sqrt{\frac{27 G M}{5 R}}$
Hence, $A \rightarrow 2, B \rightarrow 1$ and $C \rightarrow 3$.