Q.
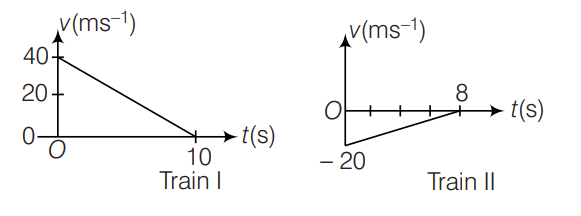
Two trains, which are moving along different tracks in opposite directions are put on the same track by mistake. On noticing the mistake, when the trains are $300\, m$ apart the drivers start slowing down the trains. The graphs given below show decrease in their velocities as function of time. The separation between the trains when both have stopped is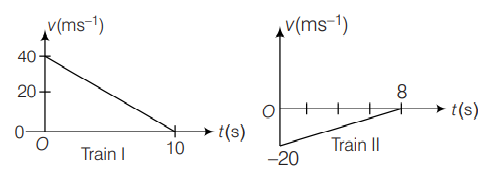
AP EAMCETAP EAMCET 2016
Solution: