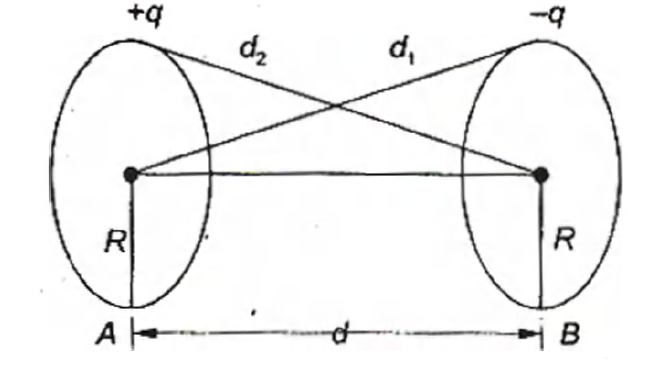
Q. Two thin wire rings each having a radius $R$ are placed at a distance $d$ apart with their axes coinciding. The charges on the two rings are $+ q$ and $- q$. The potential difference between the centres of the two rings is :
AIEEEAIEEE 2005Electrostatic Potential and Capacitance
Solution:
The electric potential at a distance $x$ from charged ring is $V =\frac{ q }{4 \pi \epsilon_{0} \sqrt{ x ^{2}+ R ^{2}}}$
Thus, the potential at the center of ring of charge $+Q=$ potential due to itself $+$ potential due to other ring of charge $- Q$.
or $V _{1}=\frac{ Q }{4 \pi \epsilon_{0} \sqrt{0^{2}+ R ^{2}}}+\frac{(- Q )}{4 \pi \epsilon_{0} \sqrt{ d ^{2}+ R ^{2}}}$
also the potential at the center of ring of charge $- Q =$ potential due to itself $+$ potential due to other ring of charge $+Q$.
or $V _{2}=\frac{(- Q )}{4 \pi \epsilon_{0} \sqrt{0^{2}+ R ^{2}}}+\frac{ Q }{4 \pi \epsilon_{0} \sqrt{ d ^{2}+ R ^{2}}}$
Thus, potential difference the center of the two rings is $V = V _{1}- V _{2}$
or $V =\frac{ Q }{4 \pi \epsilon_{0} R }+\frac{(- Q )}{4 \pi \epsilon_{0} \sqrt{ d ^{2}+ R ^{2}}}-\frac{(- Q )}{4 \pi \epsilon_{0} R }-\frac{ Q }{4 \pi \epsilon_{0} \sqrt{ d ^{2}+ R ^{2}}}=\frac{ Q }{2 \pi \epsilon_{0}}\left[\frac{1}{ R }-\frac{1}{\sqrt{ d ^{2}+ R ^{2}}}\right]$