Question

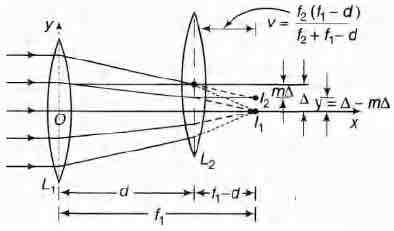
Two thin convex lenses of focal lengths $f_1$ and $f_2$ are
separated by a horizontal distance d (where d < $f_1, d < f_2)$
and their centres are displaced by a vertical separation $\Delta$ as
shown in the figure.
Taking the origin of coordinates, O, at the centre of the first
lens, the x and y-coordinatcs of the focal point of this lens
system, for a parallel beam of rays coming from the left, are
given by

• A. $x=\frac{f_1 f_2}{f_1 + f_2},y =\Delta$
• B. $x=\frac{f_1 (f_2+d)}{f_1 + f_2-d},y =\frac{\Delta}{f_1 + f_2}$
• C. $x=\frac{f_1 f_2+d(f_1-d)}{f_1 + f_2-d},y =\frac{\Delta (f_1 - d)}{f_1 + f_2-d}$
• D. $x=\frac{f_1 f_2+d(f_1-d)}{f_1 + f_2-d}, y=0$

Answer 1

Answer: (C)

From the first lens parallel beam of light is focused at its
focus i.e. at a distance $f_1$ from it. This image $I_1$ acts as virtual
object for second lens $L_2$. Therefore, for $L_2$,
$ u=+(f_1-d), f=+ f_2$
$\therefore \, \, \, \, \, \, \, \, \, \, \frac{1}{v}=\frac{1}{f}+\frac{1}{u}=\frac{1}{f_2}+\frac{1}{f_1 - d}$
Hence,$ \, \, \, \, \, \, \, v=\frac{f_2(f_1-d)}{f_2 +f_1-d}$
Therefore, x-coordinate of its focal point will be
$ x= d+ v=d+\frac{f_2 (f_1-d)}{f_2+f_1 -d}$
$ =\frac{f_1 f_2+d(f_1-d)}{f_1 +f_2-d}$
Linear magnification for $L_2$
$ \, \, m=\frac{v}{u}=\frac{f_2 (f_1-d)}{f_2+f_1-d}.\frac{1}{f_1 -d}=\frac{f_2}{f_2+f_1-d}$
Therefore, second image will be formed at a distance of m$\Delta$
or $\big(\frac{f_2}{f_2+f_1-d}\big).\Delta$below its optic axis.
Therefore, y-coordinate of the focus of system will be
$ y=\Delta -\big(\frac{f_2 \Delta}{f_2+f_1-d}\big)$
or $ y=\frac{(f_1-d). \Delta}{f_2+f_1-d}$