Q.
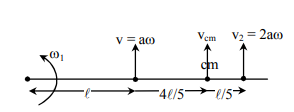
Two thin circular discs of mass $m$ and $4\, m$, having radii of $a$ and $2 a$, respectively, are rigidly fixed by a massless, rigid rod of length $l=\sqrt{24}$ a through their centers. This assembly is laid on a firm and flat surface and set rolling without slipping on the surface so that the angular speed about the axis of the rod is $\omega$. The angular momentum of the entire assembly about the point 'O' is $\vec{ L }$ (see the figure). Which of the following statement(s) is(are) true?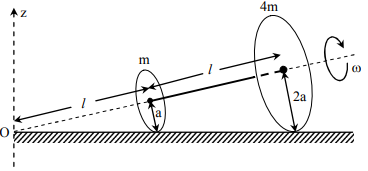
JEE AdvancedJEE Advanced 2016
Solution: