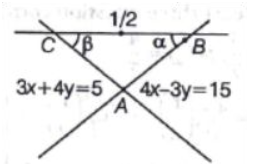
Question

Two straight lines $3 x+4 y=5$ and $4 x-3 y=15$ intersect at the point $A$. The equations of the lines passing through $(1,2)$ and intersecting the given lines at $B$ and $C$ such that $A B=A C$ are

• A. $x+4 y=9,4 x-y=2$
• B. $9 x-2 y=5,2 x+9 y=20$
• C. $6 x-y=4, x+6 y=13$
• D. $7 x+y=9, x-7 y+13=0$

Answer 1

Answer: (D)

Given line
$3 x+4 y=5$ and $4 x-3 y=15$
Slope of line $3 x+4 y=5$ is
i.e., $m_{1}=\frac{-3}{4}$
Slope of line $4 x-3 y=15$
i.e., $m_{2}=\frac{4}{3}$

Let the slope of line $B C=m$
Given, $A B=A C$
$\because \tan \alpha=\tan \beta$
$\frac{m-\frac{4}{3}}{1+\frac{4 m}{3}}=\frac{-\frac{3}{4}-m}{1-\frac{3 m}{4}}$
$\frac{3 m-4}{3+4 m}=\frac{-3-4 m}{4-3 m}$
$12 m^{2}-9 m^{2}-16+12 m$
$=-9-12 m-12 m-16 m^{2}$
$\Rightarrow 7 m^{2}+48 m-7=0$
$\&\,\,(7 m-1)(m+7)=0$
$\&\,\, m=\frac{1}{7}, m=-7$
Equation of line passing through $(1,2)$ and slope $\frac{1}{7}$ is,
$=y-2=\frac{1}{7}(x-1)=x-7 y+13=0$
Equation of line passing through $(1,2)$ and slope $=-7$ is
$y-2=-7(x-1)$
$7 x+y=9$