Q.
Two straight conducting rails form a right angle as shown below. A conducting bar in contact with the rails starts at the vertex at time $t =0$ and moves with constant velocity of $v=5 m / s$ along them. A magnetic field with $B=0.1 T$ is directed out of the page. The absolute value of the emf around the triangle at the time $t=4 s$ will be?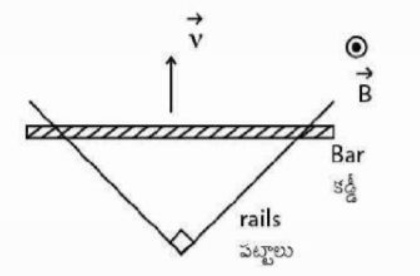
TS EAMCET 2020
Solution:
