Q.
Two stones are thrown up simultaneously from the edge of a cliff $200\, m$ high with initial speeds of $15 \,ms ^{-1}$ and $30 \,ms ^{-1}$.
Taking $g=10\, ms ^{-2},$ the graph of relative position of the second stone with respect to the first has been shown. The equation of the curved part is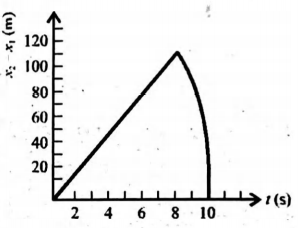
Motion in a Straight Line
Solution: