Q.
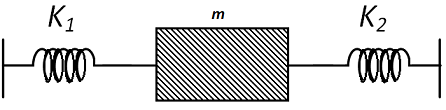
Two springs of force constants $K_{1}$ and $K_{2}$ , respectively, are connected to a mass $m$ , as shown. The frequency of oscillation of the mass is $f$ . If both $K_{1}$ and $K_{2}$ are made four times their original values, the frequency of oscillation becomes
NTA AbhyasNTA Abhyas 2020Oscillations
Solution:
