Q.
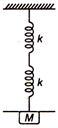
Two springs having force constants $k$ each are arranged in parallel and in series. A mass $M$ is attached to two arrangements separately. If time period in first case is $T_{1}$ and in second case is $T_{2}$, then ratio $\frac{T_{1}}{T_{2}}$ is :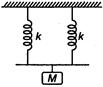
Bihar CECEBihar CECE 2003Oscillations
Solution:

