Q.
Two springs are connected to a block of mass $M$ placed on a frictionless surface as shown below. If both the springs have a spring constant $k$, then the frequency of oscillation of the block is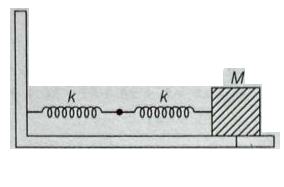
ManipalManipal 2016
Solution: