Question

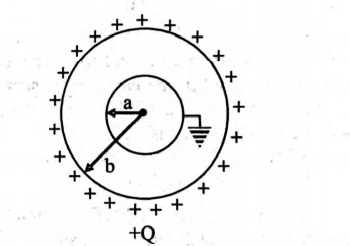
Two spherical conductors $A$ and $B$ of radii a and $b(b>a)$ are placed concentrically in air. $B$ is given a charge $+ Q$ and $A$ is earthed. The equivalent capacitance of the system is -

• A. $4 \pi \varepsilon_{0}\left[\frac{ ab }{ b - a }\right]$
• B. $4 \pi \varepsilon_{0}[ a + b ]$
• C. $4 \pi \varepsilon_{0} b$
• D. $4 \pi \varepsilon_{0}\left(\frac{b^{2}}{b-a}\right)$

Answer 1

Answer: (D)

The charge $Q$ given to outer sphere distributes as $Q_{1}$ outside and $Q_{2}$ inside which induces charge $-Q_{2}$ on outside of inner sphere, $+Q_{2}$ on inside of inner sphere which is earthed.
The inside of outer and the inner sphere constituting a spherical condenser having capacitance $4 \pi \epsilon_{0} \frac{ ab }{ b - a }$ and the outside of the outer constitutes an isolated sphere of capacitance $4 \pi \epsilon_{0} b$.
$\therefore $ the effective capacitance is
$4 \pi \epsilon_{0} \frac{a b}{b-a}+4 \pi \epsilon_{0} b$
$=4 \pi \epsilon_{0} b\left[\frac{a}{b-a}+1\right]$
$=4 \pi \epsilon_{0} b\left[\frac{a+b-a}{b-a}\right] $
$C=4 \pi \epsilon_{0} \frac{b^{2}}{b-a}$