1. Tardigrade
  2. Question
  3. Physics
  4. Two spherical bodies of mass M and 5M and radii R and 2R respectively are released in free space with initial separation between their centres equal to 12 R. If they attract each other due to gravitational force only, then the distance covered by the smaller body just before collision, is :

Question Error Report

Thank you for reporting, we will resolve it shortly

Back to Question

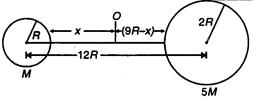
Q. Two spherical bodies of mass M and 5M and radii R and 2R respectively are released in free space with initial separation between their centres equal to 12 R. If they attract each other due to gravitational force only, then the distance covered by the smaller body just before collision, is :

WBJEEWBJEE 2006

Solution:

Let at O there will be a collision. If smallersphere moves $ x $ distance to reach at $ O, $ thenbigger sphere will move a distance of $ (9R-x). $
$ F=\frac{GM\times 5M}{{{(12R-x)}^{2}}} $ $ {{a}_{small}}=\frac{F}{M}=\frac{G\times 5M}{{{(12R-x)}^{2}}} $ $ {{a}_{big}}=\frac{F}{5M}=\frac{GM}{{{(12R-x)}^{2}}} $ $ x=\frac{1}{2}{{a}_{small}}{{t}^{2}}=\frac{1}{2}\frac{G\times 5M}{{{(12R-x)}^{2}}}{{t}^{2}} $ ?(i) $ (9R-x)=\frac{1}{2}{{a}_{big}}{{t}^{2}}=\frac{1}{2}\frac{GM}{{{(12R-x)}^{2}}}{{t}^{2}} $ ?(ii) Thus, dividing Eq. (i) by Eq. (ii), we get $ \frac{x}{9R-x}=5 $ $ \Rightarrow $ $ x=45R-5x\Rightarrow 6x=45R $ $ \therefore $ $ x=7.5R $

Solution Image