1. Tardigrade
  2. Question
  3. Mathematics
  4. Two spheres of radii 3 and 4 cut orthogonally The radius of common circle is

Question Error Report

Thank you for reporting, we will resolve it shortly

Back to Question

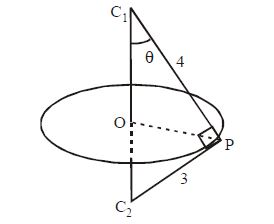
Q. Two spheres of radii 3 and 4 cut orthogonally The radius of common circle is

Three Dimensional Geometry

Solution:

For the orthogonal section $C_1P$ and $C_2P$ are pendicular where $C_1$ and $C_2$ are centres of sphere of radii $4$ and $3$ respectively
Now $C_1P = 4$ and $C_2P = 3$, so $tan\,\theta = \frac{3}{4}$
$\therefore $ Radius of circle of intersection
$OP = C_{1}P \,sin \, \theta = 4 \times \frac{3}{5} = \frac{12}{5}$

Solution Image